论文：http://arxiv.org/abs/2310.02391
源码：https://github.com/dreamfold/foldflow
license：CC BY-NC-SA 4.0

FoldFlow算法是一种针对$\text{SE(3)}^N$分布定制的连续归一化流。算法通过条件流匹配（Conditional Flow Matching，CFM）来实现最优路径的学习。每个残基在空间中各种可能刚性分布构成一个SE(3)群，算法正是从N个残基的SE(3)中寻找一种合理的分布。

算法解析

由于算法涉及比较多的黎曼几何（Riemannian Geometry）中关于黎曼流形（Riemannian Manifolds）的原理，这里只能粗浅的根据本人理解做出表达。

SE(3)刚体运动群

每个残基的骨架是N、CA、C和O这四个原子构成，由于酰胺键的特点，其中CA-C-O会和下一个原子的N构成一个平面，运动时是一个刚性整体（其他单键的两个原子也是一个刚体）。这些刚体在空间中的旋转和平移构成了一个SE(3)刚体运动群分布。而本文的目标就是能够基于现有的PDB数据，构建一个生成合理分布的模型。SE(3)可以解构为SO(3)旋转群和三维空间的半直积，从而可以在分析时将旋转平移分离。

$$\text{SE(3)}\cong \text{SO(3)}\ltimes(\mathbb{R}^3, +)$$

黎曼流形中的flow match

和在欧几里得空间中类似，我们可以定义黎曼流形$\mathbb{M}$中任意点$x$的概率分布$\rho(x)$。对于一个连续时间$t$中，从$\rho_o$到$\rho_t$的一个变化叫做流。一般算法中t会归一化，也就是$t\in [0,1]$。算法也就是希望训练一个流形向量场（本质上是类似MD的力场），从$\rho_0$流动得到最终合理稳定的$\rho_1$。

这个问题可以抽象为下列常微分方程（ODE），其中$\psi(x)$为状态函数，$\psi_0(x)=x$，$u$向量场函数，ODE代表的是在t时刻的一个瞬时状态。

$$\frac{d}{dt}\psi_t(x)=u(\psi_t(x))\$$

理论上可以通过预定义向量场并进行simulation来得到 $\rho_1$，但是这是十分time cost而且需要准确的预定义（本质上就是MD了），

因此算法采用了一个流匹配（flow match，FM）的想法，通过将t时向量场 $ut$ 参数化为
$v{\theta}(t, x_t)$ 近似 $u_t$。

但是因为先验的$u_t$ 是不可知的，
因此利用PDB数据进行后验 $u_t(x|z)$ 的近似，也就是优化下列目标：

$$L_{rcfm}(\theta)=\mathbb{E}_{t,q(z),\rho_t(x_t|z)}||v_{\theta}(t,x_t)-u_t(x_t|z)||_g^2$$

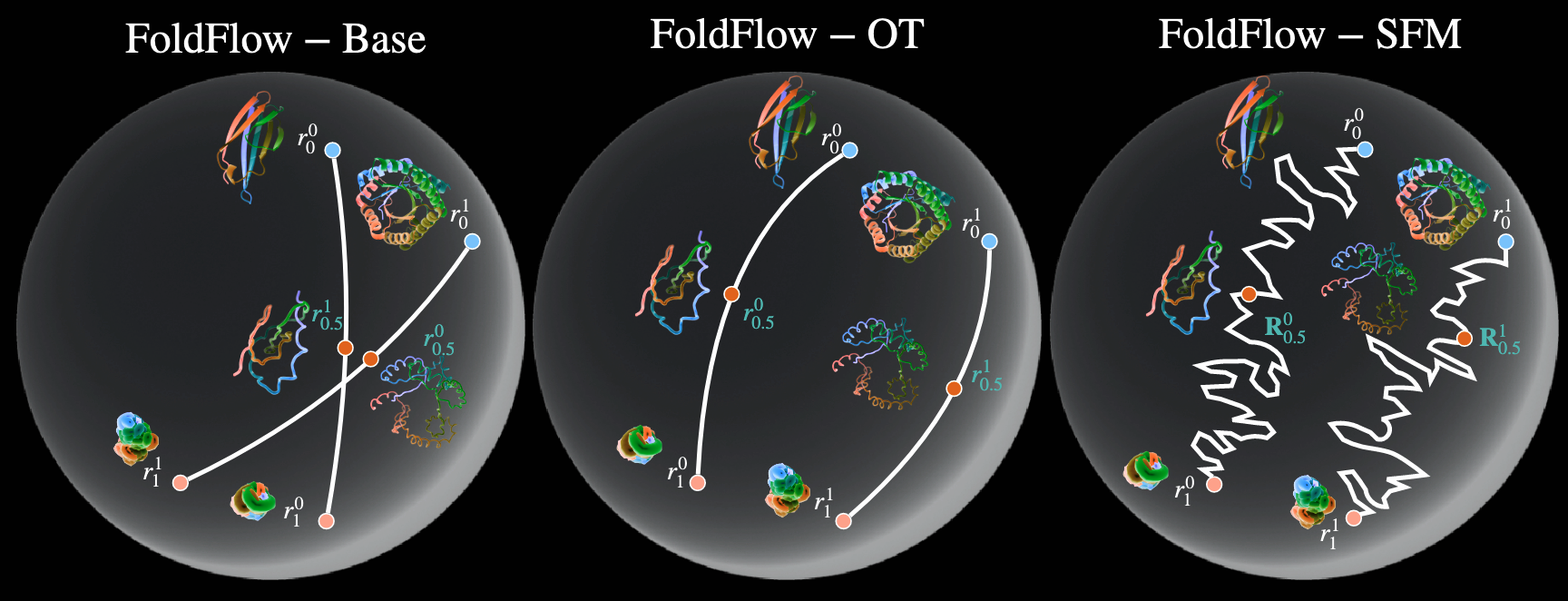
FoldFLow模型

base

基础的一个版本，确定性的流过程。

$$L_{FOLDFLOW_BASE-SO(3)}(\theta)=\mathbb{E}_{t\sim U(0,1),q(r_0,r_1),\rho_t(r_t|r_0,r_1)}||v_{\theta}(t,r_t)-\log_{r_t}(r_0)/t||_{SO(3)}^2$$

OT

增加了最优运输的分布约束

SFM

在OT的基础上引入了SDE

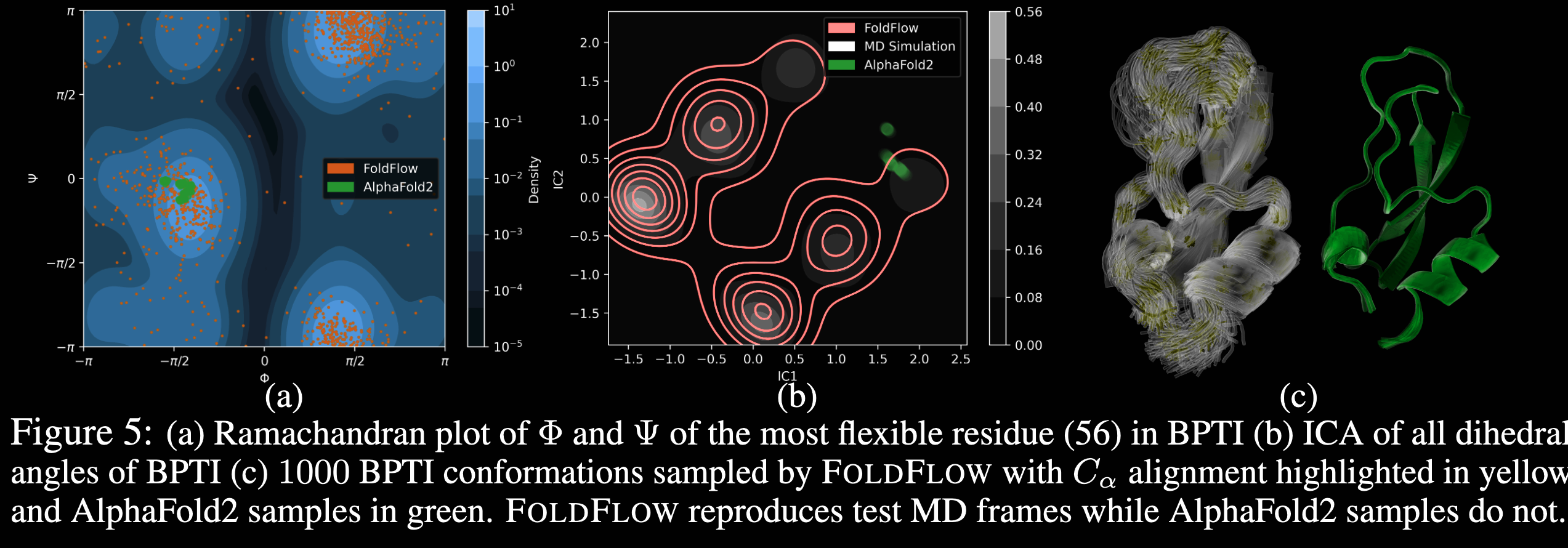
性能展示

可以看到从结果性能来看，RFdiffusion还是更胜一筹，而且目前框架不能像RFdiffusion那样进行给定靶点的binder骨架设计，需要进行必要的二次开发。
但是相比RFdiffusion，FoldFlow提供一种新的技术路线，而且其在多构象采样上有更好的潜力。相比RFdiffusion从随机分布的扩散生成，FoldFlow是一种基于黎曼流形的运动变化流，因此它可以接受输入构象进行二次采样，类似MD的动力学模拟。从作者展示的效果来看，算法有一定的构象采样能力。